[LLM] Graphormer 훑어보기
그래프 단위에서 Transformer의 가능성을 검증한 Graphormer에 대해서 알아봅니다.
원제: Do Transformers Really Perform Bad for Graph Representation?
본 포스트는 Graphormer (Do Transformers Really Perform Bad for Graph Representation?) 논문을 리뷰한 내용을 포함하고 있습니다. 원문은 여기에서 보실 수 있습니다.
Contents
1. Introduction - 트랜스포머, 그래프에 진짜 안돼?
오늘은 추천을 위한 Link prediction에 적용되는 GNN이 아닌, 화학 분야에서 주로 다루어지는 그래프 자체의 표현 학습(graph representaion learning)에 특화된 Graphormer라는 모델에 대해 살펴보겠습니다.
해당 논문의 도입은 다음과 같이 시작됩니다.
다른 도메인(자연어나 비전)에서 트랜스포머는 너무 잘 작동했음. 그런데 graph representaion learning에서는 안되는게 미스테리 하잖아? 우리가 그 미스테리를 해결해 보려고!
다른 데에서 잘 작동했으니 여기서도 잘 될거야! 라는 다소 무모(?)한 확신으로 시작하고 있지만, 확실히 다른 데이터 도메인에서의 혁신적인 성공에 비해 그래프 분야에서는 트랜스포머가 충분히 빛을 보이지 못한 것 같습니다. 저자들은 이런 확신을 증명이라도 하듯이 Graphormer라는 모델로 Transformer 방법론의 강력함을 다시 한 번 증명해 보이는데요.
2. Transformer 돌아보기
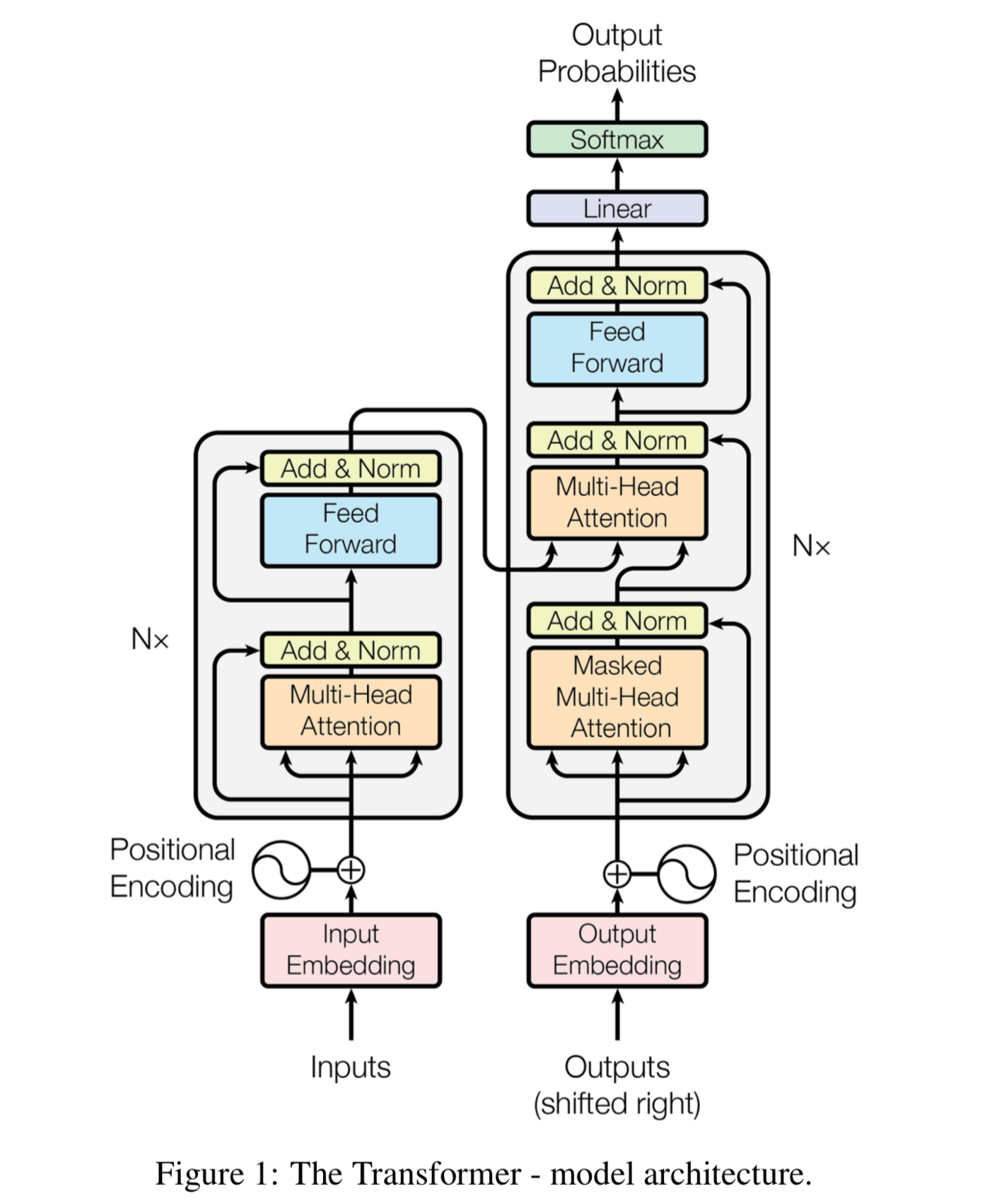
Transformer에 대해 다시 살펴 보고 넘어갈까요?
Transformer는 2017년에 공개된 Self-attention 기반 모델입니다. 자연어처리 분야에서 BERT, GPT 등 대형 언어 모델의 핵심 블록으로 사용되어 그 효율성이 입증된 이후로, 컴퓨터 비전, 강화학습, 추천시스템 등의 타 분야도 활발히 연구와 적용이 이루어지고 있는데요. 2022년 10월 현재 기준 무려 52,845건이 인용된 인싸중의 인싸 알고리즘입니다.
2-1. Transformer의 성공 비결: self-attention
Transformer가 자연어처리 분야의 SOTA를 갈아치우며 주목을 끌게 된 데에는, 그 핵심적인 아이디어인 self-attention에 있습니다. self-attention이란, 말 그대로 모델이 스스로 어떤 것에 주목해야 하는지를 알아서 학습한다는, 개념 그 자체로 딥러닝스러운 학습 방법인데요.
2-2. Self-attention의 직관적인 설명
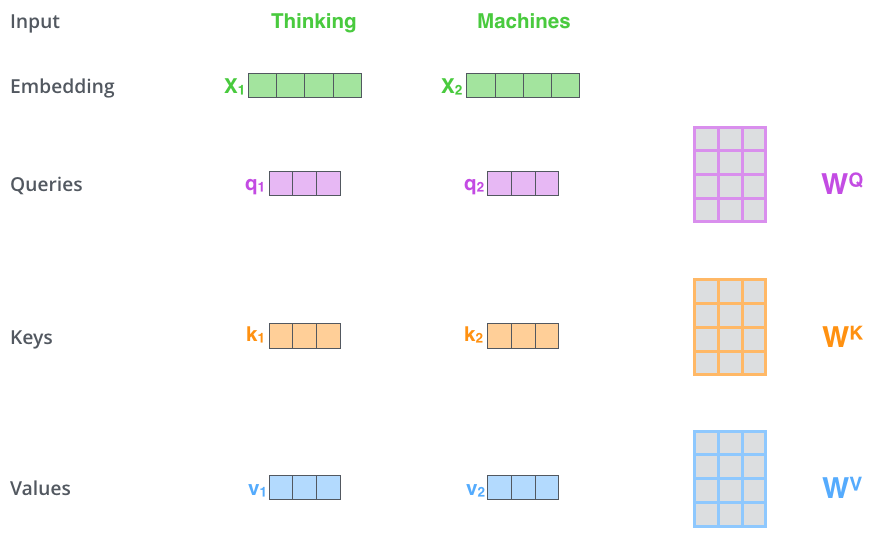
Q(Query), K(Key), V(Value)가 주어졌을 때 Q와 K의 내적으로 구한 attention score, 즉 유사도 값을 기반으로 해당 key를 나타내는 representation인 Value를 얼마만큼 주목해서 볼 것인지를 결정하게 되는 방법입니다.
가령 [“안녕”, “나는”, “러닝머신”,”이야”]라는 시퀀스가 있을 때, “나는”이라는 단어가 주어졌을 때 어떤 단어를 주목해서 봐야할지를 찾아낸다고 해보겠습니다.
“나는”이라는 단어가 내가 알고 싶은 질의 단어이기 때문에 Query는 “나는”이 되고, 얼마나 주목할지 알고 싶은 대상인 다른 단어들 [“안녕”,”러닝머신”,”이야”]는 그들과의 유사도를 계산하는데 사용할 Key의 주인이자 representation인 Value의 주인이라고 할 수 있겠습니다.
여기서 “나는”이라는 단어와 다른 단어와의 유사도를 “나는”의 query 벡터와 다른 단어들의 key 벡터를 내적함으로써 계산합니다. 그 결과를 합이 1이 되도록 표준화(softmax)하니, [0.2, 0.7, 0.1]이라는 값이 나왔다고 해보겠습니다. 이 결과로써 나온 저 값을 attenion score라고 하고, 이들만큼의 가중치를 두어 각 단어들의 value를 크게 반영하여 다음 레이어에 전달합니다.
2-3. Self-attention의 성공 비결
이와 같은 방식이 성공한 이유는, Transformer 이전에 많은 성공을 이루어 낸 기존의 두 방법론의 한계를 극복한 것에서 찾아볼 수 있을 것 같습니다.
1) CNN의 local receptive field 극복
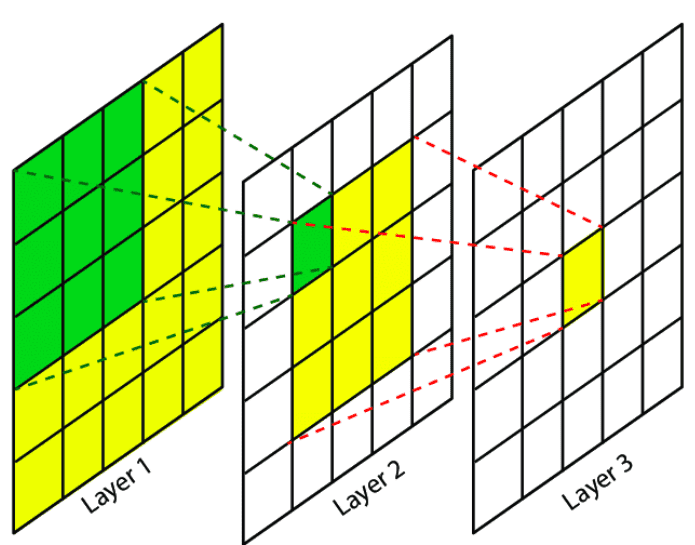
CNN의 경우 자신의 주변에 있는 픽셀들의 정보만을 받아들임으로써, 지역적인 receptive field를 사용한다는 특징이 있습니다. 이러한 특징은 연산을 효율적으로 만들고, 또 직관적으로 국소적인 유의미한 패턴을 감지해낸다는 점에서 큰 이점이 있었으나 전체적인 큰 그림을 보지는 못한다는 한계가 있었습니다.
transformer는 전체 개체들에 대해 전역적인, 즉 global receptive field를 가짐으로써 CNN이 나무만을 보고 있을 때 숲을 함께 볼 수 있는 시야를 가졌다는 장점을 가질 수 있었습니다.
2) RNN의 단방향적 정보 습득 방식 극복
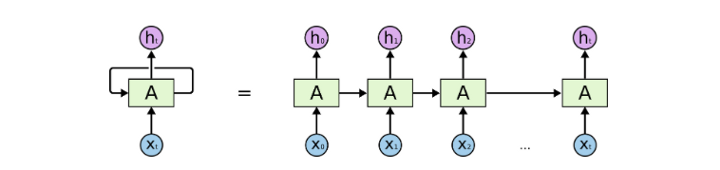
RNN의 경우 순방향, 혹은 역방향으로 단방향의 정보를 확인했습니다. attention을 활용해 이러한 접근으로 발생하는 정보 손실을 줄이기는 했으나, transformer는 구조적으로 양방향으로 정보를 얻어옴으로써 정보 손실을 줄일 수 있었습니다.
2-4. GNN에서 self-attention 방식의 적용
기존의 CNN 방법론을 그래프 표현 학습에 적용한 GCN의 학습 방식을 떠올려보면, 앞서 살펴본 장점을 GNN에서도 얻을 수 있을 것이라고 기대해볼 수 있습니다.
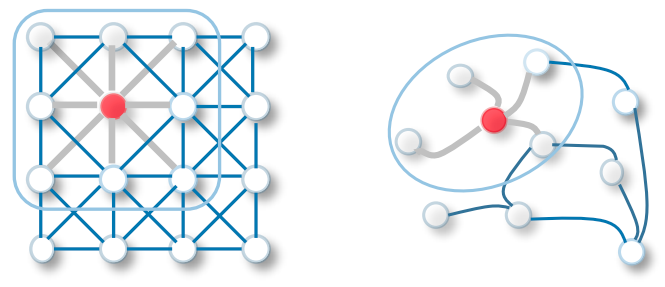
GCN의 경우 여러 개의 Convolution Layer를 쌓음으로써 multi-hop의(여러 다리를 걸쳐 떨어진) 이웃의 정보를 가져옵니다. Convolution Layer는 지역적인 이웃의 정보를 살펴 aggregation하는, local receptive field를 갖는 전파 방식이라고 생각할 수 있겠습니다.
반면 transformer 기반 방법은 global하게 전체 노드와의 중요도를 살펴보아 attention score로 직접적으로 정보를 가져 오는 접근일 것이며, 이러한 방식을 적용함으로써 CNN의 한계를 Transformer가 극복했듯이 얼마간의 학습 효율을 가져올 수 있을 것이라고 생각해볼 수 있겠죠.
기존 GNN은 인접행렬을 통해 edge 정보(연결 여부)를 받아옴으로써 그래프 구조 정보를 반영하여 network를 학습했습니다. graph에 transformer를 적용하게 된다면 NLP에서 transformer를 적용할 때도 그러하듯이, 위치 정보 및 연결 정보를 반영한 positional encoding 같은 역할을 하는 정보가 함께 사용되어야 하겠죠. Graphormer는 이러한 위치 인코딩 방식을 어떻게 비유클리드적으로 정의되는 그래프 구조에서 적용할 수 있을지에 대한 해결책을 제시합니다.
3. Graphormer란?
3-1. Motivation
앞서 언급했듯이, Graphormer는 그래프 자체의 표현 학습인 Graph representaion learning에 강점을 가진 방법론입니다. 일반적인 GNN 방법론은 node의 representation을 얻어 이들의 label을 분류하거나(node classification) 이렇게 얻은 node representation을 활용해 유사도를 구하여 link를 예측하는(link prediction) 문제를 풀어 왔습니다.
그런데 그래프 자체의 구조의 표현을 사용해야 하는 경우에는 어떨까요?
가령, 네트워크 내의 군집이 있을 때 이들이 어떤 동아리인지를 분류한다거나, 분자 구조가 주어졌을 때 화학적인 어떠한 특성을 예측해 낸다거나 하는 작업이 있을 것입니다.
기존에는 node와 edge의 표현을 잘 통합하는 Readout function에 통과시킴으로써 그래프 자체의 임베딩을 얻어 내는 방식을 사용했습니다. Sum/Mean과 같은 단순한 함수를 사용하기도 하고, GIN(Graph Isomorphism Network)에서는 FC Layer (Fully-Connected Layer)를 학습하여 어떤 이상적인 Readout Function을 근사하는 방법을 시도하기도 하였습니다.
그러나 Readout Function을 걸치는 과정에서 어떠한 정보 손실, 혹은 노이즈가 발생할 수도 있을 것 같습니다. 가령 노드의 임베딩을 평균으로, 즉 readout function을 mean으로 사용한다면, 분명히 다른 특색을 가진 그래프임에도 불구하고 동일한 임베딩을 갖게되는 경우를 생각해볼 수 있겠죠.
따라서 이러한 한계점을 극복하고자, 여기에 Transformer를 적용해서 그래프 자체를 통째로 표현해보자! 라는 것이 Graphormer의 아이디어입니다.
3-2. Graphormer의 특징

Transformer는 그래프를 나타내는 모든 node와 edge를 하나의 context로 표현할 수 있습니다. transformer가 주로 사용되었던 자연어 데이터에 대입해보면, node는 문장의 토큰을, edge는 문장 구성 요소(토큰)간의 의미상 연결 관계로 바라볼 수 있습니다. self-attention을 통해 문장이라는 그래프를 구성하는 node와 edge의 의미적인 표현을 얻어낸다고 생각해 볼 수 있겠죠.
Graphormer는 이러한 transformer에 그래프의 구조적인 특징을 반영할 수 있는 구조를 개발했습니다. 여기서 그래프의 구조적인 특징이란, 첫째로 위치 정보가 없다는 점(즉, 그래프 구성요소에는 순서가 없다는 것)과 둘째로 edge를 통한 연결 정보만 존재할 뿐, 거리 정보는 없다는 점 등을 들 수 있습니다.
기존의 GNN 방법론은 multi-hop의 정보를 받아들이도록 학습하기 위해, 노드 단위로 학습이 이루어진 뒤 1-hop의 정보를 여러 layer로 쌓았습니다. 그러나 이는 직접으로 layer마다 연결된 노드끼리의 정보를 활용한다는 점에서 local한 접근으로 볼 수 있습니다.
반면에 Graphormer는 transformer의 구조를 사용해 multi-hop의 정보를 self-attention을 통해 한번에 학습합니다. 즉, global한 접근으로 multi-hop 정보를 학습합니다.
Attention을 Graph에 적용한 Graph Attention Network (GAT) 역시 Transformer와 유사한 구조를 띠고 있습니다. 그래프를 구성하는 노드별로 representation이 주어졌을 때, 앞서 설명한대로 query와 key matrix를 만들어 이들의 내적을 통해 attention score를 구한 뒤, 이들을 weight로써 사용하는 방법론입니다. GAT는 adjacency matrix 내에서 연결 정보에 따라서 masking된 매트릭스를 사용합니다. 즉, 연결된 노드에 대해서만 attention score를 구합니다.
transformer는 이러한 attention 구조에 positional encoding이 추가되어 있습니다. 또, 전체 node에 대해서 attention을 수행하기 때문에, masking이 없다는 차이점이 있습니다. 더불어 GAT는 subgraph를 대상으로 연산이 이루어지는 반면 transformer는 전체 그래프를 입력으로 받습니다.
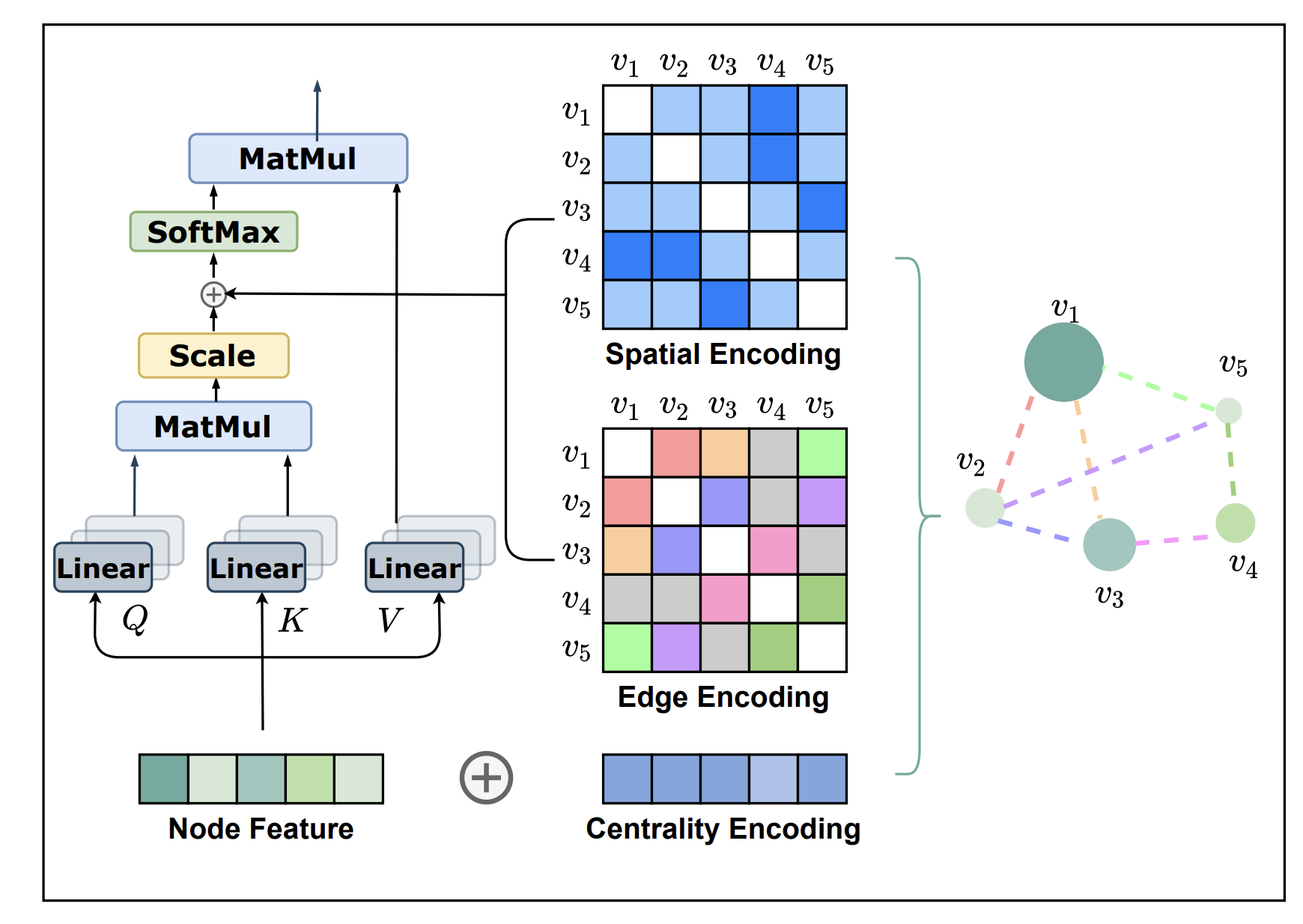
Graphormer 모델은 이와 같은 transformer block을 사용하고, node feature로는 random하게 initialization한 값을 사용합니다. 여기에, 뒤에서 설명할 3가지 방법의 인코딩(centrality, edge, spatial encoding) 을 적용함으로써 graph의 구조적인 정보를 임베딩에 반영합니다.
4. Graphormer의 세가지 인코딩 방법
4-1. Centrality encoding
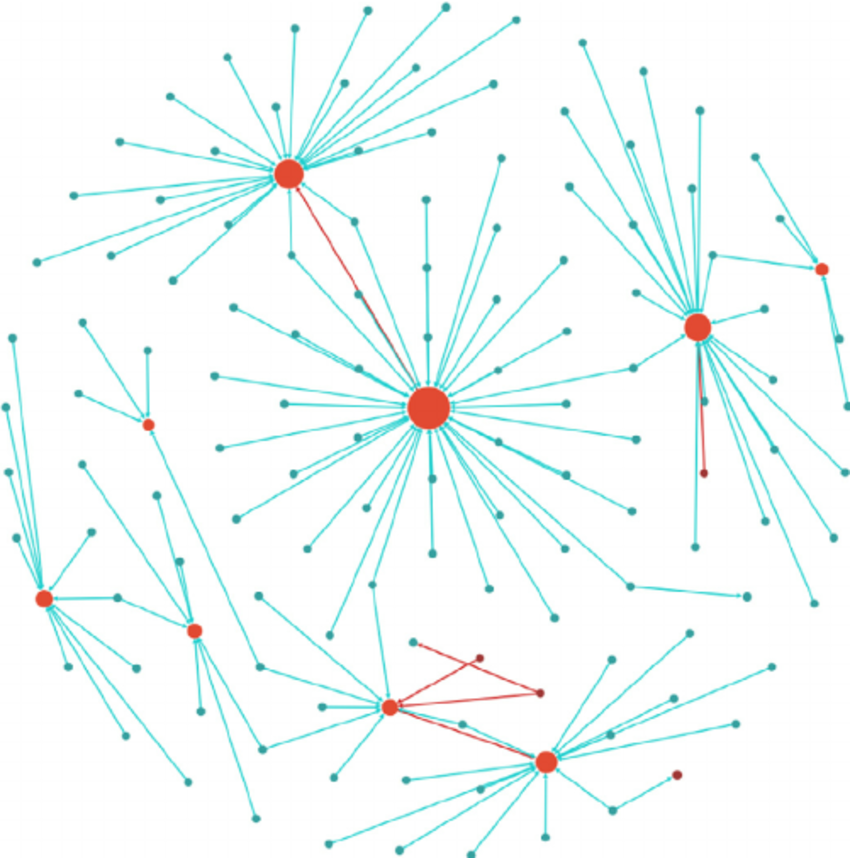
Centrality encoding은, 그래프 내 중심성을 반영하는 방법입니다. 그래프 내에서 어떤 노드가 중심인지를 나타내는 데 사용되는 지표로는, degree(노드에 연결된 엣지의 개수), betweeness(두 노드가 연결될 때 한 노드를 지나간다면 그 사이에 얼마나 가중치가 있는가를 측정), closeness, page rank, eigenvalue 등이 있습니다.
그래프에는 허브 노드가 존재합니다. 이러한 허브 노드는 우리가 풀고자 하는 다양한 문제에서 다른 일반적인 노드에 비해 상대적으로 더 큰 중요성을 갖습니다. 가령, 인스타 팔로워가 많은 셀럽이 소셜 네트워크의 트렌드 예측에 더 중요한 것처럼 말이죠.
그런데, self-attention은 centrality 정보를 충분히 담지 못합니다. 그래프를 구성하는 노드들 간의 중요성을 나타내는 attention score는 해당 노드가 전체 그래프 관점에서 갖는 중요도를 충분히 반영하기 못하기 때문이라고 이해할 수 있겠습니다.
Graphormer에서는, centrality encoding을 degree값을 사용하여 나타냈습니다. 초기에 random init하기 때문에 중요한 허브 노드가 무시되는 것을 방지하기 위해, degree를 이용해 초기에 가중치를 제공하고 그 이후에는 learnable parameter를 학습 시킴으로써 그 인코딩된 정보를 업데이트 해나가는 방식으로 학습합니다.
여기서는 방향성 역시 고려하는데, in-degree emb와 out-degree emb를 따로 사용하여, 두개의 합을 centrality로 정의합니다. 한쪽으로 편향된 노드의 경우 허브 노드로 간주하기 어려울 것 같습니다. 무작정 following만 수 만명을 클릭한 유저를 인스타그램 트랜드 예측에 중요한 허브 노드로 볼 수 없는 것처럼 말이죠. 이러한 방법으로, 의미의 유사성(노드 피처를 통해)과 노드의 중요도(centrality encoding을 통해)를 고려한 attention을 얻을 수 있게 됐습니다.
4-2. Spatial Encoding
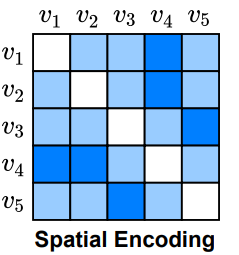
고차원 공간 상에 표현되는 노드의 위치 정보를 활용한다면, 더 나은 그래프의 임베딩을 얻을 수 있을 것 같습니다. 그런데, 그래프 내에서는 유클리드 거리를 사용할 수 없기 때문에 절대적인 거리 measure를 사용할 수 없습니다. 기존의 BERT에서는 sequential한 데이터에 위치 정보를 반영하기 위해 relative positional encoding을 사용했습니다. Graphormer에 적용된 relative positional encoding은 Edge를 통해 연결된 정보를 기반으로, 노드 간의 거리를 측정하는 방법입니다.
relative positional encoding 적용을 위해, 먼저 두 노드 간 최단 거리(shortest path)를 사전에 계산 해 놓습니다. transformer layer에서는 모든 노드에 대한 정보를 한번에 받기 때문에, 상대적 거리에 따른 attention이 달라져야 합는데, 이렇게 미리 구해 놓은 거리 정보를 spatial encoding으로 이용함으로써 그래프의 구조적 정보를 반영해 학습하게 됩니다.
4-3. Edge Encoding
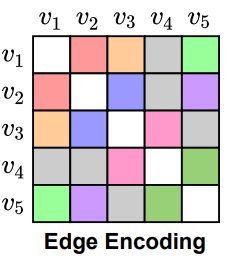
Graphormer는 단순히 노드 정보만으로 그래프의 임베딩을 얻는 것이 아니라, Edge의 정보 또한 반영함으로써 노드 간의 상관관계를 녹여내려고 했습니다. 가령 분자 구조의 경우 일반 결합, 이중 결합처럼 다른 연결 특성이 있을 때 이를 고려한 표현을 얻어내는 것이 타당하겠죠. 단순히 연결 여부만을 binary로 표현하는 것이 아닌, 이러한 다양한 연결 정보를 다르게 처리하는 것이 필요해 보입니다.
먼저 최단거리를 구성하는 edge의 평균을 통해 두 노드의 관계를 표현합니다. 가령, 1-3-4번 노드를 지나가는 edge를 표현한다고 했을 때, edge feature 값을 random하게 초기화합니다.
최단거리를 구성하는 edge의 평균을 통해 두 노드의 관계를 표현하는 방법에 대해서 설명하겠습니다.
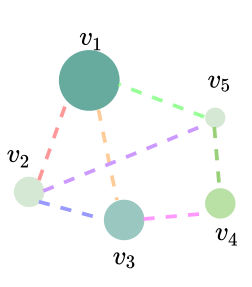
위의 그림에서, 1-3-4번 노드를 지나가는 edge를 표현한다고 해보겠습니다. e_1, e_2가 주어졌다고 합시다. 각각 노드1-노드3 사이, 노드3-노드4 사이에 있는 엣지입니다. 먼저, edge feature의 초기 값을 random하게 초기화합니다.
shortest path에 있는 feature SP_1이 있습니다. 이 SP_1을 edge feature와 내적해 스칼라 값을 가져옵니다. 또, 마찬가지로 e2와 SP_2를 내적해 스칼라 값을 가져옵니다. 이 둘을 평균 내 줌으로써 edge encoding의 값 E_14를 얻습니다. edge의 feature를 통해 특징을 표현하고, shortest path 내에 있는 노드의 피처를 반영한 결과를 얻어 내게 됩니다.
4-4. Special Node
Graphormer에서는 위의 3가지 encoding 방법과 더불어 Special Node를 적용하여 더욱 정밀한 그래프 표현을 학습해 냅니다. Special Node란, 그래프 내의 전체 노드와 연결되는 가상의 노드를 의미합니다. readout function을 사용하는 대신, special node를 도입하여 전체 그래프의 표현을 담아냅니다. 이는 BERT의 CLS 토큰과 유사한 역할을 한다고 생각해볼 수 있습니다.
이러한 노드를 [Vnode] (=virtual node)로 표기합니다. 이 [Vnode]는 일반 노드처럼 앞서 설명한 인코딩 과정을 똑같이 수행하게 됩니다. 이 때, spatial encoding에서 다른 값으로 처리함으로써 실제로 존재하는 허브 노드와는 구별됩니다.
학습 시, [Vnode] 값을 통해 Graph Classification을 진행합니다. BERT의 CLS 토큰이 문장 전체의 임베딩을 담아내어 Text Classification과 같은 downstream task를 수행하는데 사용되는 것과 동일한 방식입니다. 이 [Vnode]를 self-attention 없이 사용하게 된다면, over smoothing 문제가 발생하게 됩니다. 즉, 전체 노드에 연결되어 있는 [Vnode]의 특성 상 여러 관계 없는 노드들 사이를 연결짓게 되고, 그 결과 각 노드의 표현을 얻어냄에 있어 차별화 되지 않는, 지나치게 서로 비슷한 결과를 얻게 되는 것입니다. 반면에 self-attention을 사용하여 적절한 weight를 가하여 aggregation한다면, 그래프를 대표할 수 있는 정보를 모든 노드에서부터 적절히 가져올 수 있음을 의미합니다. 이렇게 얻어진 [Vnode]를 통해 그래프를 대표할 수 있는 표현을 얻게 되고, 이로써 다양한 graph level의 task를 효과적으로 수행할 수 있다고 합니다.
개선을 위한 여러분의 피드백과 제안을 코멘트로 공유해 주세요. 내용에 대한 지적, 혹은 질문을 환영합니다.
출처
https://www.youtube.com/watch?v=G2PoGAyg-1k&t=1672s

Leave a comment